Problem
Let $\infty$ and $-\infty$ denote two distinct objects, neither of which is in $\mathbb{R}$.
Define an addition and scalar multiplication on $R \cup {\infty} \cup {-\infty}$ as you could guess from the notation. Specifically, the sum and product of two
real numbers is as usual, and for $t \in \mathbb{R}$ define
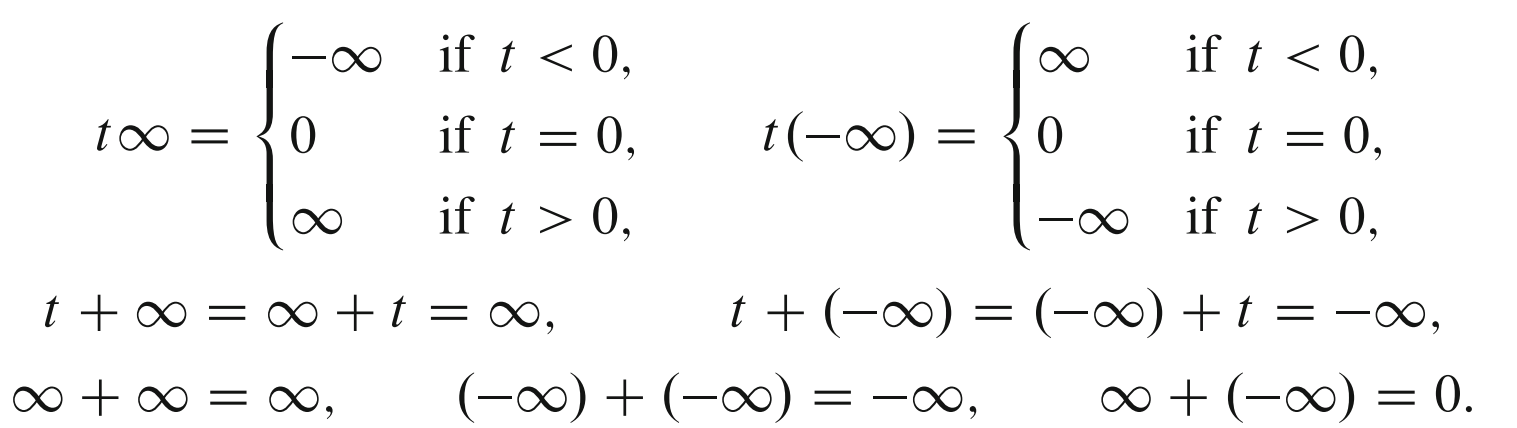 Is $\mathbb{R} \cup {\infty} \cup {-\infty}$ a vector space over $\mathbb{R}$? Explain.
Is $\mathbb{R} \cup {\infty} \cup {-\infty}$ a vector space over $\mathbb{R}$? Explain.
Solution
No, because: $$1 = 1 + 0 = 1 + (\infty - \infty) \stackrel{D1.19}{=} (1 + \infty) - \infty = \infty - \infty = 0$$ Which is a contradiction, since the $0$-“vector” is unique by theorem 1.25.