Problem
For each of the following subsets of $\mathbb{F}^3$, determine whether it is a subspace of $\mathbb{F}^3$:
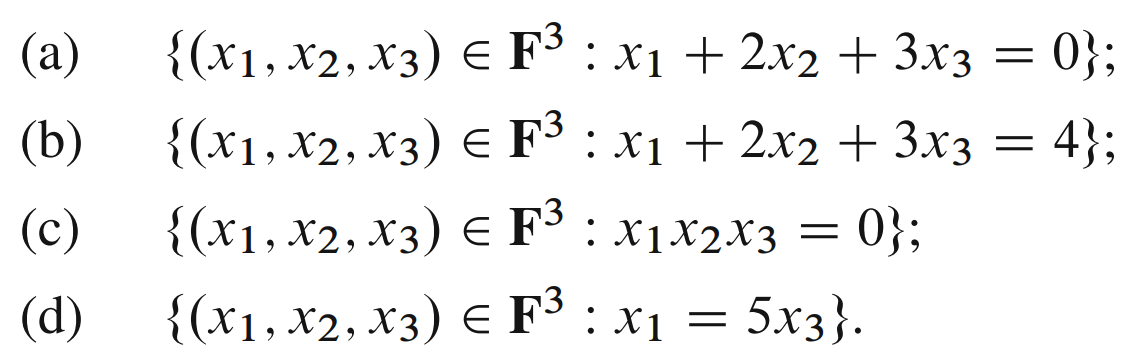
Solution
We need to varify the 3 conditions for a subset of a vectorspace to be a subspace given in theorem 1.34 for each of the four given subsets.
Subset (a)
- The additive identity $(x_1, x_2, x_3) = (0,0,0) = 0$ is in the subset because $0 + 2 \cdot 0 + 3 \cdot 0 = 0$.
- Now let $x = (x_1, x_2, x_3)$ and $y = (y_1, y_2, y_3)$ be elements of the subset (a), then $x + y \stackrel{D1.12}{=} (x_1 + y_1, x_2 + y_2, x_3 + y_3)$ will also be in (a), since $(x_1 + y_1) + 2(x_2 + y_2) + 3(x_3 + y_3) \stackrel{P1A9 \land P1A4}{=} (x_1 + 2x_2 + 3x_3) + (y_1 + 2y_2 + 3y_3) = 0 + 0 = 0$, thus the subset (a) is closed under addition.
- Also $\lambda x = \lambda (x_1, x_2, x_3) \stackrel{D1.17}{=} (\lambda x_1, \lambda x_2, \lambda x_3)$ is in the subset (a) for all $\lambda \in \mathbb{F}$ because $(\lambda x_1) + 2(\lambda x_2) + 3(\lambda x_3) \stackrel{P1A9 \land P1A6 \land E1.4}{=} \lambda (x_1 + 2x_2 + 3x_3) = \lambda 0 = 0$
From the three points above we see that subset (a) is a subspace of $\mathbb{F}^3$.
Subset (b)
The subset (b) is not a subspace of $\mathbb{F}^3$, because $(x_1, x_2, x_3) = (0,0,0) = 0$ is not an element of the subset $0 + 2 \cdot 0 + 3 \cdot 0 \neq 4$.
Subset (c)
The subset (c) is not a subspace of $\mathbb{F}^3$, because $x = (1,1,0)$ and $y = (0,1,1)$ are both in the set (c), but $x + y = (1,1,1)$ is not since $1 \cdot 1 \cdot 1 \neq 0$, therefore subset (c) is not closed under addition.
Subset (d)
- The additive identity $(x_1, x_2, x_3) = (0,0,0) = 0$ is in the subset (d), as $0 = 5 \cdot 0$.
- Let $x = (x_1, x_2, x_3)$ and $y = (y_1, y_2, y_3)$ be in the subset (d), thus $x_1 = 5x_3$ and $y_1 = 5y_3$, then $x + y \stackrel{D1.12}{=} (x_1 + y_1, x_2 + y_2, x_3 + y_3)$ is in (d) because $x_1 + y_1 = 5x_3 + 5y_3 \stackrel{P1A9}{=} 5(x_3 + y_3)$.
- Also $\lambda x \stackrel{D1.12}{=} (\lambda x_1, \lambda x_2, \lambda x_3)$ with $\lambda x_1 = \lambda (5x_3) \stackrel{P1A6 \land E1.4}{=} 5 (\lambda x_3)$
From the three points above we see that subset (a) is a subspace of $\mathbb{F}^3$.