Problem
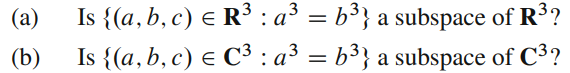
Solution
Subset (a)
In $\mathbb{R}$, the function $f(x) = x^3$ is injective and thus $a^3 = b^3 \iff a = b$. Therefore the subset of $\mathbb{R}^3$ we’re dealing with is $\lbrace {x,x,y} \in \mathbb{R}^3 | x,y \in \mathbb{R} \rbrace$ which is a subspace:
- $0 = (0,0,0)$ is in the subset, this is when $x=y=0$
- $(x_1,x_1,y_1) + (x_2,x_2,y_2) \stackrel{D1.12}{=} (x_1 + x_2, x_1 + x_2, y_1 + y_2)$ and since we clearly have $x_1 + x_2 = x_1 + x_2$, the subset is closed under addition.
- Let $\lambda \in \mathbb{R}$, then $\lambda (x,x,y) \stackrel{D1.17}{=} (\lambda x, \lambda x, \lambda y)$ and since clearly $\lambda x = \lambda x$, the subset is closed under scalar multiplication.
Subset (b)
In $\mathbb{C}$, the function $f(x) = x^3$ is not injective and thus $a^3 = b^3 \cancel{\iff} a = b$. Therefore we have that both $(1,e^{i\frac{2\pi}{3}},0)$ and $(e^{i2\frac{2\pi}{3}},e^{i\frac{2\pi}{3}},0)$ are elements of the subset, but their sum isn’t: $$(1,e^{i\frac{2\pi}{3}},0) + (e^{i2\frac{2\pi}{3}},e^{i\frac{2\pi}{3}},0) = (1 + e^{i\frac{2\pi}{3}}, 2e^{i\frac{2\pi}{3}}, 0)$$ Implying equality at $\spadesuit$ if the subset (b) is a subspace: $$1 + 3e^{i2 \cdot \frac{2\pi}{3}} + 3e^{i\frac{2\pi}{3}} + 1 = \left(1 + e^{i\frac{2\pi}{3}}\right)^3 \stackrel{\spadesuit}{=} \left(2e^{i\frac{2\pi}{3}}\right)^3 = 8$$ Which is clearly not the case, as this would imply $2 = e^{i2 \cdot \frac{2\pi}{3}} + e^{i\frac{2\pi}{3}} = - 1$, which is a contradiction, thus subset (b) is NOT a subset.