Problem
Suppose $U$ is a subspace of $V$ with $U \neq V$. Suppose $S \in \mathcal{L}(U,W)$ and $S \neq 0$ (which means that $Su \neq 0$ for some $u \in U$). Define $T: V \to W$ by:
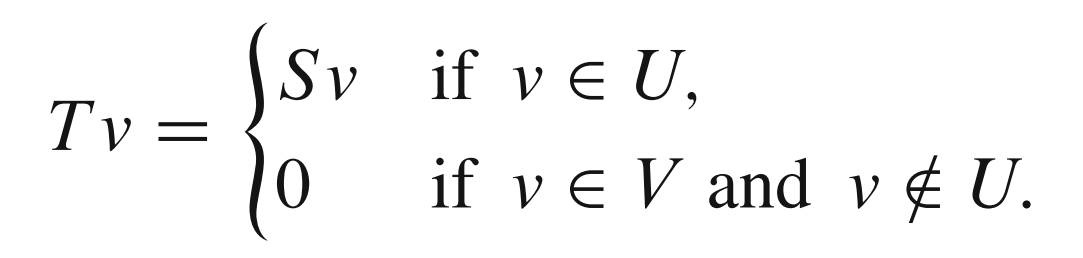
Prove that $T$ is not a linear map on $V$
Solution
Let $u \in U$ and $v \in V$ such that $v$ $\cancel{\in}$ $V$, the existence of which follows from $U \neq V$. Then if we assume $v + u \in U$, the fact that $U$ is closed under addition then implies $v = (v + u) - u \in U$, which is a contradiction. Therefore if $v$ and $u$ is defined as done above, we must have $v + u \in V$ and $v + u$ $\cancel{\in}$ $U$.
This implies that: $$0 = T(v + u) = Tv + Tu = 0 + Su = Su$$ Therefore $Su = 0$ for all $u \in U$, implying $S = 0$, a contradiction.